2019-IJCAI-[PULD]Positive and Unlabeled Learning with Label Disambiguation

https://www.ijcai.org/proceedings/2019/0590.pdf

Introduction

PUのアルゴリズムは、「信頼できるNをUから選び出して、PN Learningに帰着」、「二値分類のNoisy Labelsの問題だが、PがUになるLabel Noiseを持つ特殊なNoisy Labelsの問題とみなす」、「仮定をもとにPとUに異なる重みを与える不偏推定関数を考えそれを最小化する」の考えがある。

だが、不偏推定関数ベースの手法は、UnlabeledのデータをPとUの混合と考えている以上、どうしてもラベル付けが曖昧な点が生まれてしまう。それを必ず一方の問題設定にまとめることにより、

これについて提案手法は、Partial Label LearningというUデータを曖昧にPとNにラベルを付けてから、曖昧さをなくすアルゴリズムを使えば結果的に分類できるという手法を使う。

Method

Problem Setting

$\mathbf{x} \in \mathbb{R}^d,$ がデータであり、Ground Truthのラベルは $y=+1$ がNegative、 $y=+2$ がPositiveである。
Positiveは合計 $p$ 個存在し、 $y=+2$ からランダムで $p$ 個選ぶ。残りの $y=+2$ はすべてのNegativeと同様にUnlabeledになる。
- つまり、Single-Training-Set
識別器 $h : X \times Y \to \mathbb{R}$ を訓練したい。

提案手法の定式化

まず、KNNグラフ $G=(V,E)$ をつくる。これは正則化項で使用する。
1. $V$ はすべてのサンプル $\mathbf{x} \in X$ を頂点集合としている。
2. $E$ は各頂点 $(i,j)$ は、頂点 $i$ から近いデータの頂点 $j$ への有向辺。
  1. 類似度に関しては、 $\exp(-||\mathbf{x}_i - \mathbf{x}_j|| / (2 \delta^2))$ というガウシアンカーネル。
  2. $a_{ij}$ を以上のカーネルで構築した行列 $A$ を考える。これを対角次数行列(対角線上に各頂点の次数を持つ対角行列) $D$ によって、正規化することができる。
  $\bar{A} = D^{-1/2} A D^{-1/2}$
次に識別器は線形識別器で、 $h(\mathbf{x},y)= \boldsymbol{\omega}^T \Phi(\mathbf{x}, y)$ である。
1. $\Phi(\mathbf{x},y)$ は以下のように、 $\mathbf{x}$ をそのラベルに応じて拡張したベクトル。必ず上半分か下半分かが0である。
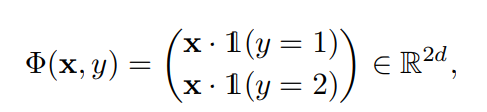
最終的には、以下の制約つき最低化問題を解く。

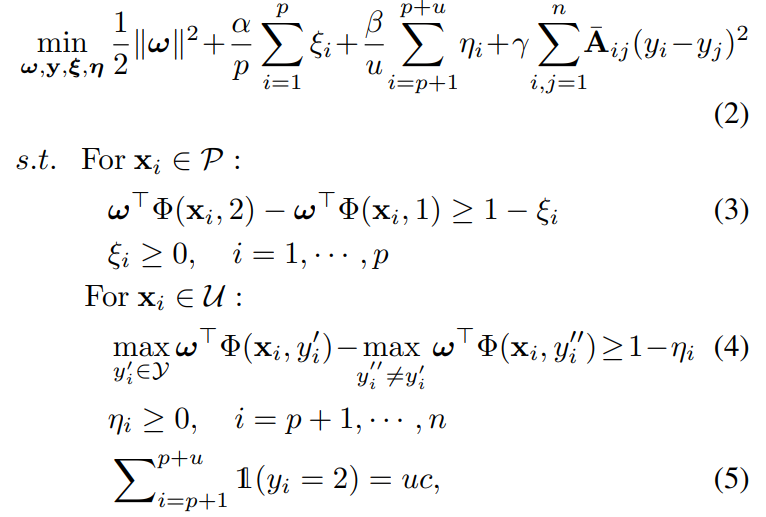
項は上から以下の意味である。
- 係数の正則化項。
- $\zeta, \eta$ はスラック変数で、それぞれPとUに該当する。
  - $\zeta$ は(3)の制約を持ち、これはPデータにおいて正しいラベルにおける評価値と誤ったラベルにおける評価値の差が $1 - \zeta_i$ 以上であるというもの。
    - $\zeta_i$ が小さければ小さいほど良い。0が一番良い。
  - $\eta$ は(4)の制約を持ち、これはUデータにおいてもっともらしいラベルにおける評価値とそうでないラベルの評価値の差が $1 - \eta_i$ 以上であるというもの。
    - $\eta_i$ が小さければ小さいほど良い。0が一番良い。
    - ここでは、識別器で予測した今の結果をさらに明確に分かれるよう、増強するようにしている。
- 類似度で似ているサンプルは、似ているラベルをお互い保持する必要がある。
そして最後の制約として、Uの中で割り当てられるPの個数は厳密に $uc$ 個でなければならない。

これはSVMで解くことができる。

なお、さらに一歩進んで、もしUの中のデータにラベルを付けることができるようになったら、以下のようにPとUをまとめて、マージン最大化するように扱える。

何かよくわからないが、結局以下の式を最適化していくそうだ。

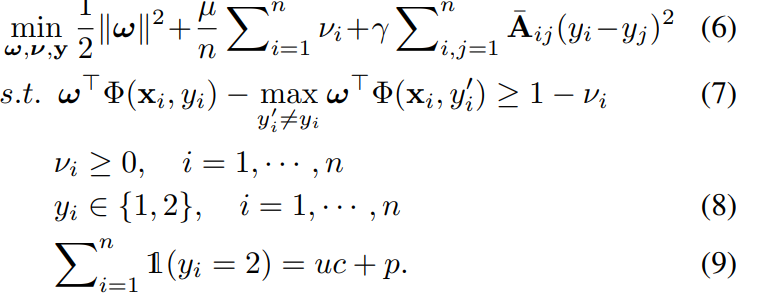
この手法は、先行研究のLapSVMと似ているが、それにはLabel Disambiguation Regularizerがない。

最適化のやり方

問題の定式化は済んだところでどのように最適化をしていくのかが焦点となる。

最適ではないが、一種類の最適化アルゴリズムを提案した。

毎アップデートごとに、ラベルが大量に変わってほしくないので、以下のように $z$ というのを導入し、最後の項で一気に変わりすぎないように制限している。

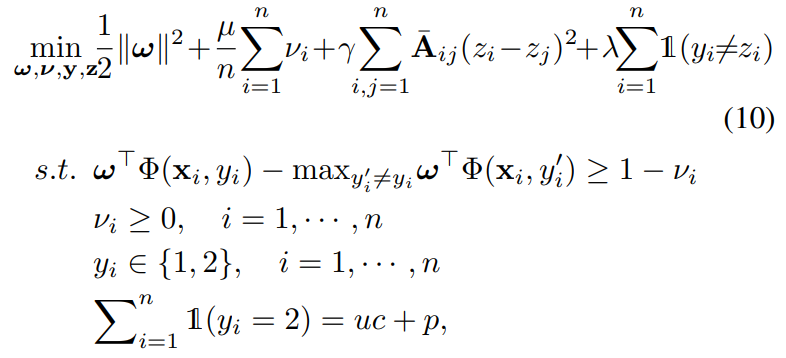
最適化の順序としては以下の順序で毎イテレーション行う。

$\boldsymbol{\omega}$ の最適化

ラベル関連の $y, z$ を固定すると最適化問題は以下のようになる。

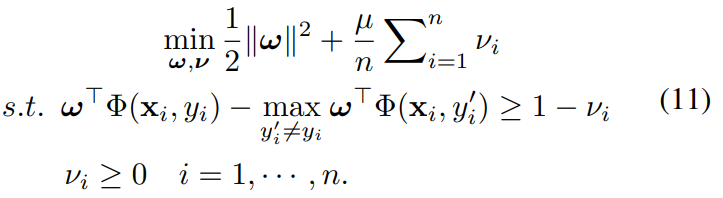
この定式化は、マルチクラスのSVMで解くことができるので、最適化できる。

$y$ の最適化

関連のない部分を消していくと以下のようになる。

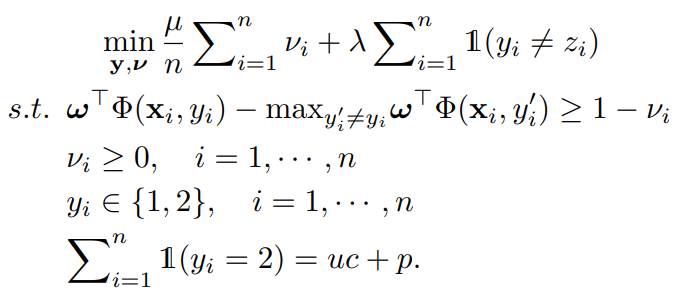
ここで、 $\nu_i$ 関連を以下のように書き直せる。つまり、PとU関連のものを統合した $\nu$ に対して、条件などから外して代入したもの。

\zeta_i^{y_i} = \boldsymbol{\omega} ^T \Phi(\mathbf{x}_i, y_i) - \max_{y_i ^\prime \neq y_i} \boldsymbol{\omega}^T \Phi(\mathbf{x}_i, y_i ^ \prime) \\ \nu_i = \max(0, 1 - \zeta_i ^ {y_i})

次に、ラベル関連の $Y$ と $Z$ についてone-hot化けさせた行列を考える。 $Y$ は $n\times 2$ の行列で、各行はサンプル $\mathbf{x}_i$ に対してのone-hotな $y, z$ の表現である。

次に、 $C$ という係数行列を定義する。これは $n \times 2$ の行列で以下のようなもの。これの目標は、以下のような $\sum_{i, j} Y_{ij} C_{ij}$ を最小化させたいこと。なので間違った予測には大きくなるように仕向けたい。

$i$ 行目は2つの要素からなり、気持ちとしてはPの該当度合いとNの該当度合いの2つの要素を持つ。

Pに含まれるデータならばNの該当度合いは $M$ と固定して、Pの該当度合いは1からPositiveだと置いた時のMarginである。
- $M$ は十分に大きい定数にすることで、予測器に絶対にこれはNだと予測させないようにできる。
Uに含まれるデータは、それぞれNの該当度合いは1からNと置いた時のMarginを引く、Pの該当度合いは1からPと置いた時のMarginを引く。
- つまり、予測Marginが大きいほど、係数が小さくなる。ラベルがone-hotになっている以上、 $1$ がかかる部分の係数を小さくしたい=正解となっている部分のMarginを小さくしたい。

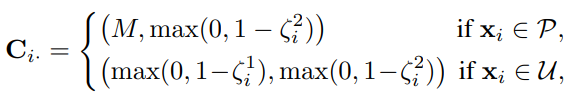
これで掛け合わせるとき、一番最初の定義はそれぞれ以下のように言い換えられる。

\min_{\mu} \frac{\mu}{n} \sum_{i=1}^n \nu_i = \min_{Y} \frac{\mu}{n} \sum_{i=1}^n \max(0, 1 - \zeta_i^{y_i}) = \min _Y \frac{\mu}{n} \sum_{i=1}^n \sum_{j=1}^2 Y_{ij} C_{ij} \\ \min_y \lambda \sum_{i=1}^n \mathbf{1}[y_i \neq z_i] \Leftrightarrow - \min_Y \lambda \sum_{i}^{n} \sum_{j=1}^2 Y_{ij} Z_{ij}

結合させると、最初の最適化問題は以下のように帰着できる。

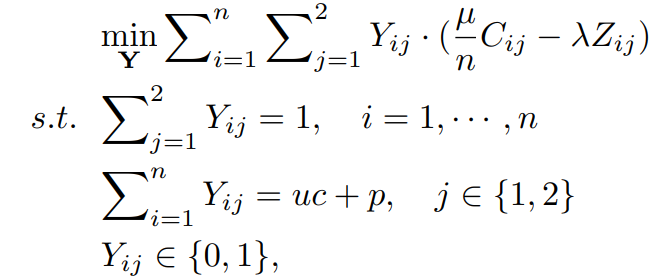
これは整数最適化問題(Yが0,1しかとらない)となるが、連続値に和らげることで線形計画問題にすることができる。

$z$ の更新

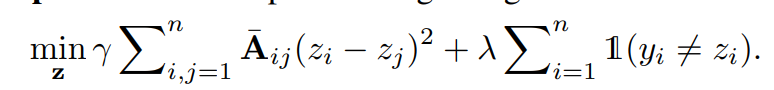
関係ある部分の式を抜き出すとこのようになる。これを行列で書き換えると以下のようになり、これの最小化は数学的に解くことができる。

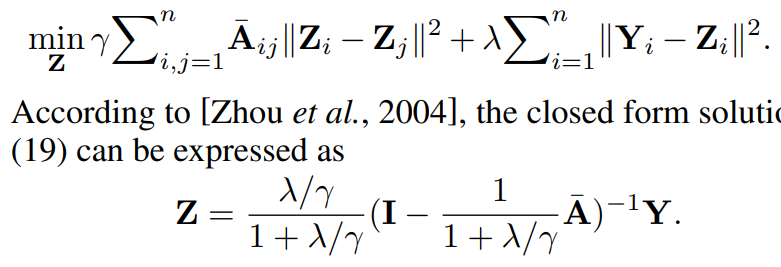
アルゴリズムの流れ

隣接があまり変わらないという項を作るために正規化した隣接行列 $\bar{A}$ をつくる。
係数行列を初期化する。Pならば(0, 1)、Uなら半半にしている。
1. Pの設定は第一成分を大きくする7行目のイテレーションとは異なるが、(0,1)にすることで、y=(1,0)であることから、何があっても $Y_{ij} C_{ij}=0$ に最初のイテレーションは固定している感じ。
線形計画法で $Y$ を決定する。
Loop内。 $\Omega, C, Y, Z$ の順番に毎イテレーション最適化する。

理論分析

Rademacher複雑度などで分析している、省略。

実験

これはSVMなどを用いて線形計画問題を解いてたりしているので、複雑なデータセットにおいてはDNNによって抽出した表現を用いた表現学習を行っている。